Crimping and deployment of metallic and polymeric stents -- finite element modelling
Abstract
Aim: This paper aims to compare the mechanical performance of metallic (Xience) and bioresorbable polymeric (Elixir) stents during the process of crimping and deployment.
Methods: Finite element software ABAQUS was used to create the geometrical models and meshes for the balloon, stent and diseased artery. To simulate the crimping of stents, 12 rigid plates were generated around the stent and subjected to radially enforced displacement. The deployment of both stents was simulated by applying internal pressure to the balloon, where hard contacts were defined between balloon, stent and diseased artery.
Results: Elixir stent exhibited a lower expansion rate than Xience stent during deployment. The stent diameter achieved after balloon deflation was found smaller for Elixir stent due to higher recoiling. Lower level of stresses was found in the plaque and artery when expanded by Elixir stent. Reduced expansion, increased dogboning and decreased vessel stresses were obtained when considering the crimping-generated residual stresses in the simulations.
Conclusion: There is a challenge for polymeric stents to match the mechanical performance of metallic stents. However, polymeric stents impose lower stresses to the artery system due to less property mismatch between polymers and arterial tissues, which could be clinically beneficial.
Keywords
Introduction
Over the past three decades, significant improvements have been made in stent designs and materials, especially the development of drug-eluting stents (DESs, approved by Food and Drug Administration (FDA) of USA in 2002). The vast majority of DESs used so far have non-degradable polymer coatings, incorporated with anti-proliferative drugs, to overcome the notorious in-stent restenosis (ISR) that represented an undesired drawback of bare metal stents.[1] Although ISR rates can be substantially reduced by DESs (lowered by 74% in high-risk patients), the life-long presence of metallic alloy stents, under loads and corrosive conditions, could increase the risk of strut fracture and failure with time. This may lead to possible complications such as delayed healing, lethal migration and unstable angina.[2,3] Bioresorbable stents provide the advance of overcoming these possible long-term complications of metallic stents. Biodegradable polymers are the most promising materials investigated to date.[4-6] Fully expandable polymeric biodegradable stents initially support the vessel wall as scaffolds with sufficient radial strength to prevent mechanic recoil after implantation. In about 6 months, arterial remodelling enters a stable phase, and no substantial scaffolding is required. Consequently, it is desirable for stents to dissolve after 6 months in the body, leaving behind an intact vessel with no pro-inflammatory substances or obstacles for future treatments.[7] During the process, the polymers gradually soften, which allows for a smooth disappearance of high stresses, imposed by the permanent stents, in the recovering artery. It should be noted that recent reports have suggested an independent relationship between bioresorbable stents and stent thrombosis.[8] Instead, the higher incidence rates of stent thrombosis were associated with the 2.5 mm platforms.[9]
One of the major concerns for polymeric BRSs is their mechanical performance, especially their interaction with blood vessels during and after deployment. Agrawal et al.[10] carried out the earliest work in assessing the in vitro performance of the Duke biodegradable stents made of Poly-L lactide (PLLA) fibres. Results showed that a successful biodegradable stent could be achieved by carefully balancing the mechanical properties of PLLA fibres and geometrical design of stents. Nuutinen et al.[11] conducted in vitro tests of a woven fibre polymeric braided stent subjected to radial compression. The performance of such stents was not as good as metal ones, and the collapse pressure was found lower, even for thicker PLLA fibres. Bünger et al.[12] compared the in vivo performance of stents made of biodegradable PLLA and stainless steel, by monitoring the stents after the implantation in carotid arteries of living pigs. Both stents achieved initial technical success. However, PLLA was reported to be significantly softer than metallic alloys, which affected the radial stiffness of the implanted stents and needed to be further investigated. Over the last two decades, great effort has been made for the development of bioresorbable stents, and there have been many devices available in preclinical and clinical evaluations. Elixir DESolve (Elixir Medical Corporation, USA) stent, made of PLLA, is one of the major biodegradable stents currently available on the market. The polymer stents showed sufficient radial strength within 6 months of implantation, with the occurrence of bioresorption between one and two years.[13]
Finite element (FE) analyses have been largely used in modelling of stent expansion and deformation during the deployment process.[14-16] However, majority FE analyses were performed on metallic stents. For example, Imani et al.[17] modelled the effects of design on vessel wall stresses for Palmaz-Schatz, Xience V and NIR stents. The comparative study confirmed that Palmaz-Schatz stent generated 15.6% and 7.6% higher stresses in the arterial wall than Xience V stent and NIR stent, respectively. The results suggested a direct correlation between vessel wall stresses and in-stent restenosis rate, as Palmaz-Schatz stent gave the highest restenosis rate in clinical trials. Recent FE simulations on metallic stents by Schiavone et al.[18] also confirmed that stent design is a major factor that controls the expansion of the device and also the stresses generated in the artery. In addition, shape optimization of metallic stents, in terms of improved fatigue resistance and radial flexibility, can also be achieved by FE modelling.[19] On the contrary, there is very limited work dedicated to modelling the deformation of bioresorbable polymer stents, particularly during the process of deployment in diseased arteries.
In this paper, FE modelling was carried out to simulate the deployment of Elixir polymer stent in a diseased artery, with head-to-head comparison against Xience metallic stent. Particularly, the simulations considered the crimping step, which is necessary to fix the as-produced stent to the catheter. The mechanical performance of the two stents has been compared directly, in terms of radial expansion and stresses in the stent-vessel system. In addition, results were also compared with those obtained without considering the residual stresses generated from the crimping process.
Methods
Models for stents, balloon and artery
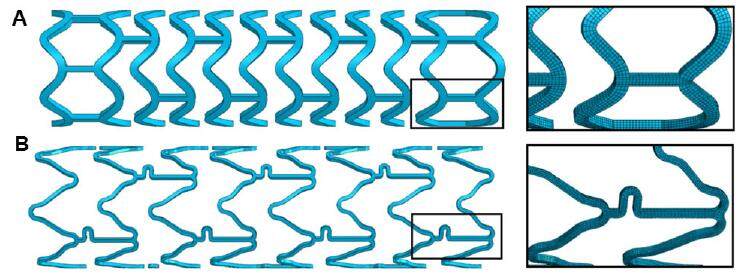
Geometries for Xience and Elixir stents were built using the NX design software. Both stents were created in expanded shape, with a diameter of 3 mm and a length of 10 mm. The geometries of both stents were based on dimensions found in open resource. The strut thickness is 80 µm and 150 µm for Xience stent and Elixir stent, respectively. The FE mesh contains eight-node incompatible brick elements, with full integration (C3D8I). The incompatible mode is chosen for the purpose of modelling large bending deformation during stent crimping and subsequent expansion. There are 4-layer elements through the width and the thickness of all struts. The geometrical designs and FE meshes for both stents are given in Figure 1.
The balloon used to inflate the stents had a tri-folded geometry which was produced using the NX software. The diameter of the fully folded part is 1.25 mm and the total length of the balloon is 14 mm. To create the pattern, the tri-folded cross section was sketched first, and subsequently extruded for a length of 12 mm. Towards the ends, the balloon smoothly transits into a circle, 0.75 mm in diameter, over a length of 1 mm. This was done by using the sweeping tools in NX. The balloon was totally constrained at both ends as they are fixed to a catheter. The diameter of the expanded balloon was set to be 3 mm, matching the targeted stent or vessel diameter after deployment. Four-node shell elements, with reduced integration (S4R), were adopted to mesh the tri-folded balloon.
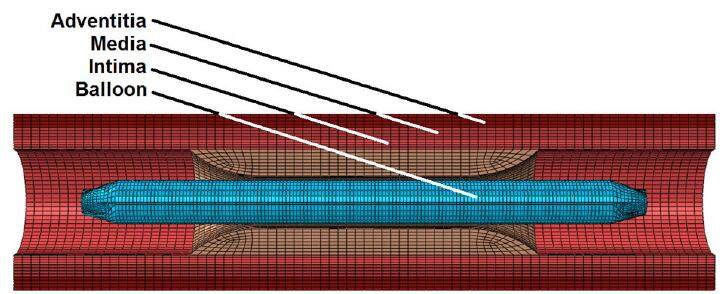
The diseased artery has a total length of 40 mm and a lumen diameter of 3 mm for the heathy part. The middle portion of the artery is covered by 10 mm plaque. The stenosis, defined as the ratio of plaque thickness to healthy lumen radius, was chosen to be 50%. The artery comprises three individual tissue layers, and the wall thickness is 0.27 mm, 0.35 mm and 0.38 mm for the intima, media and adventitia layers, respectively. Eight-node brick elements with reduced integration (C3D8R) were used to mesh the artery and the plaque. Four layers of elements were assigned through the wall of each tissue layer and eight layers of elements were assigned through the plaque thickness.
Geometry and mesh of the balloon-artery assembly are shown in Figure 2. Mesh-sensitivity studies confirmed the convergence of numerical results, with regards to stent expansion, stent recoiling and stresses in the stent-artery system, for the mesh adopted in this work.
Material model
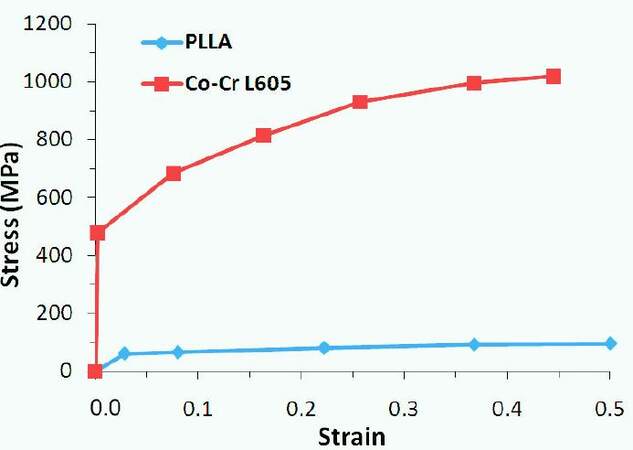
Both stents were modelled as elastic-plastic, with non-linear strain hardening [Figure 3]. The tensile stress-strain curves for Co-Cr L605 and PLLA were taken from literature.[20,21] It can be noted that PLLA is much weaker than Co-Cr L605. Table 1 gives the essential properties for both materials as obtained from the tensile curves. Strain hardening was realised in ABAQUS by stating the yield stress as a function of the plastic strain, as also obtained from the tensile curves. The plaque was assumed to be hypocellular, and its behaviour was described by the Ogden hyperelastic model. The hyperelastic model parameters were provided in Zahedmanesh and Lally.[22] The tri-folded balloon was treated as a linear elastic material. The material density, Young’s modulus and Poisson's ratio were taken as 1.1 × 106 kg/mm3, 900 MPa and 0.3, respectively.[23]
| Material | ρ (kg/mm3) | E (GPa) | ν | σy (MPa) |
|---|---|---|---|---|
| Co-Cr L605 | 9.1E-6 | 243 | 0.30 | 476 |
| Poly-L lactide | 1.4E-6 | 2.2 | 0.30 | 60 |
It is well recognised that the arterial layers possess distinct anisotropic behaviour as they are reinforced by two families of collagen fibres. Here, the established Holzapfel-Gasser-Ogden (HGO) anisotropic hyperelastic model[24] was employed to describe the anisotropic behaviour of individual coronary arterial layer. In this model, the hyperelastic strain energy potential W is given by:[24]
W = C10(I1 - 3) + (k1/2k2)[exp(k2<Ef>2) - 1] + (1/D)[(J2-1)/2 - lnJ]
Ef = κ(I1 - 3) + (1 - 3κ)(I4 - 1)
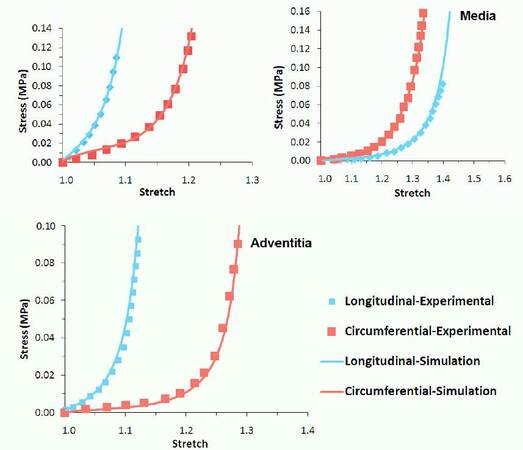
where C10, D, k1, k2 and κ are model parameters, I1 and J are the first and third stretch invariants, and I4 is the invariant of Cauchy-Green deformation tensor. The Macauley bracket is indicated by the operator <>, whilst γ represents the angle between the mean directions of the two families of fibres whose deformation is defined by Ef. The model parameters [Table 2] were calibrated against the experimental data.[25] Both longitudinal and circumferential stress-stretch responses, computed by using the HGO model, agreed with the experimental data very well[25] for all three vessel layers [Figure 4].
Parameter values of the anisotropic Holzapfel-Gasser-Ogden model for the arterial layers
| Layer | ρ (kg/mm3) | C10 | D | k1 | k2 | κ | γ |
|---|---|---|---|---|---|---|---|
| Intima | 1.066E-6 | 0.03 | 8.95E-7 | 4.0 | 1200.0 | 0.303 | 60° |
| Media | 1.066E-6 | 0.005 | 5.31E-6 | 0.57 | 80.0 | 0.313 | 20° |
| Adventitia | 1.066E-6 | 8.32E-3 | 4.67E-6 | 1.0 | 1000.0 | 0.303 | 67° |
Figure 4. Stress-stretch curves for the three artery layers: Holzapfel-Gasser-Ogden model vs. experimental data[25]
The HGO model used in this work is for incompressible hyperelastic materials. To consider compressible deformation, the HGO-C model was suggested, with the anisotropic part expressed by isochoric invariants (insensitive to volumetric deformation). However, Nolan et al.[26] found that the HGO-C model was unable to simulate compressible anisotropic behavior correctly, because it used isochoric anisotropic invariants which is insensitive to volumetric deformation. Consequently, they formulated a modified anisotropic (MA) model by using the full anisotropic invariants which accounted for a volumetric anisotropic contribution. The MA model correctly predicted the material’s anisotropic response to hydrostatic tensile loading, pure shear and uniaxial deformations. They also found the HGO-C model significantly underpredicted arterial compliance, which might affect the simulation results of stent deployment in diseased arteries. To fully clarify this effect, a considerable amount of new work is required, especially the efforts required for coding a user-defined material subroutine for the MA model (interface with the FE package Abaqus). This is beyond the scope of this paper, and will be investigated in our future studies. Nevertheless, the HGO model used in this work was calibrated properly against the longitudinal and circumferential tensile data of arteries.[25] It was proved to be a reliable anisotropic formulation for modeling deformation of the arterial layers with collagen fibre reinforcement.
Crimping simulation
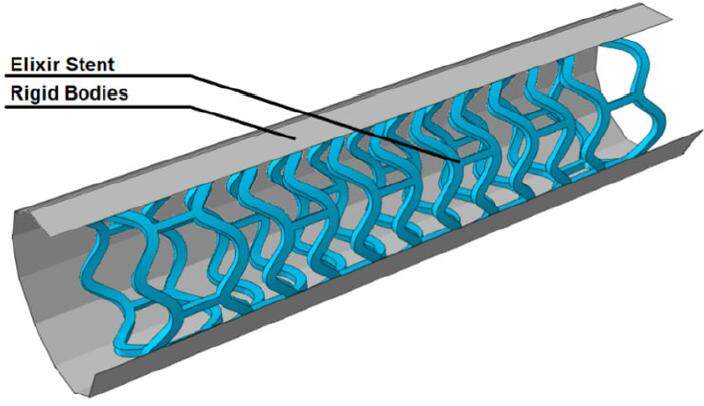
To model stent crimping, twelve rigid plates were generated around the stent as shown in Figure 5. The rigid plates were modelled as shell surfaces. Uniform radial displacement, linearly increasing to 1 mm within a step time of 0.1 s, was applied to the plates to enforce the crimping of stent. Spring back of the stent after crimping, due to the recovery of elastic deformation, resulted in a final stent diameter of 1.5 mm, which is able to fit in the diseased vessel.
Abaqus explicit was adopted for crimping simulations (0.1 s step time). No constraint was applied to the stent. Hard contact was assigned between the outer surface of the stent and the rigid plates. The friction coefficient was assumed to be 0.8. Following crimping, an additional step was used to simulate the spring back of the stent within 0.1 s. In this step, the contacts between the rigid plates and the stent were deleted, allowing for the stent to recover the elastic deformation freely.
Expansion simulation
The expansion procedure was simulated using two steps, namely inflation and deflation. During the inflation step (0.1 s), a pressure linearly increasing to 1.2 MPa was applied inside the balloon. While in the deflation step (0.1 s), the balloon pressure was brought linearly down to zero. All analyses were carried out by considering the residual stresses generated from crimping. Again, simulations were performed using the explicit solver in Abaqus. Change of stent outer diameter was tracked for the middle ring and the two end rings of both stents. The data outputs were used to quantify stent expansion as well as the recoiling and dogboning effects.[27]
Results
Stent crimping
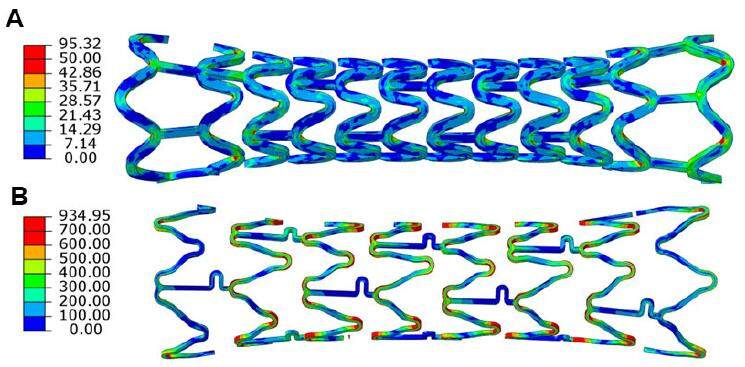
During crimping, both stents underwent severe bending deformation, as illustrated in Figure 6 for Elixir stent. The two stents were squashed to a diameter of only 1.25 mm at the fully crimped state. After crimping, stresses were highly localised at the U-bend regions for both devices. The von Mises stress in the Xience and the Elixir stents had a maximum magnitude of 750 MPa [Figure 7A right] and 96 MPa [Figure 7A left], respectively. After spring back, the maximum von Mises stress in the Xience and Elixir stents relaxed to 706 MPa and 50 MPa, respectively [Figure 7B]. These are also the residual stresses generated in the stent after crimping. And the diameter of both stents settled at about 1.5 mm.
Figure 6. Deformation of Elixir stent and balloon (A) before, (B) during and (C) at the end of the crimping process
Stent expansion
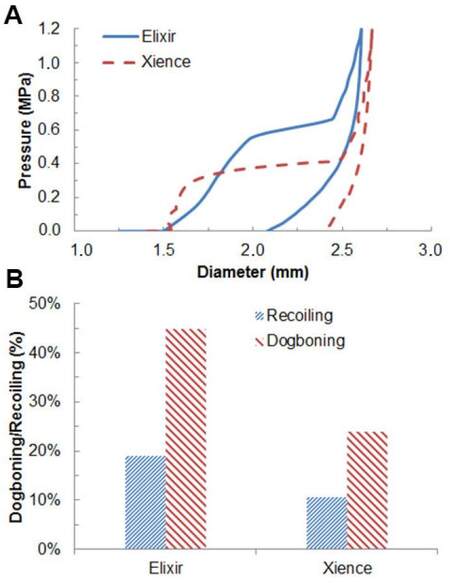
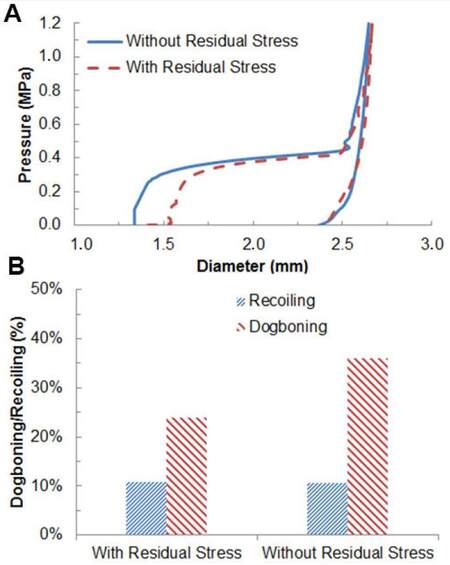
Pressure-diameter plots in Figure 8 showed that Elixir stent experienced a lower rate of expansion than Xience stent. Both stents developed a saturation state in expansion with the increasing pressure, but Elixir stent reached the saturation earlier. At the maximum pressure, the stent outer diameter was computed as 2.66 mm and 2.61 mm for the Xience and Elixir stents, respectively. The recoiling effect was 11% for the Xience stent [Figure 8B], which is significantly lower than that for the Elixir stent (20%; Figure 8B). Consequently, a larger final diameter was achieved for the Xience stent (2.40 mm) when compared to the Elixir stent (2.10 mm only). Consistently, the Xience stent also showed considerably less dogboning effect (24%) than the Elixir stent (45%).
Figure 8. (A) Diameter change against pressure; (B) recoiling and dogboning effects during deployment of Elixir and Xience stents
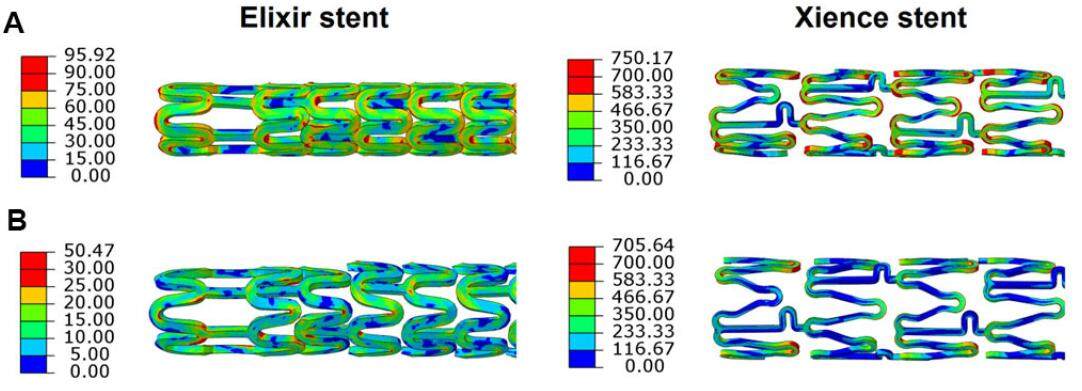
High levels of stresses were developed in both stents following their deployment in the artery [Figure 9]. Similar to the crimping process, the maximum von Mises stresses were found in the U-bend districts, with a value of 935 MPa for the Xience and 95 MPa for the Elixir stent. In the artery, the peak stresses were generally found on the plaque, especially towards the ends of the stenosis. This was caused by the dogboning effect of the implanted stent. There is a direct connection between stress concentration and localized rupture for plaque as evidenced in numerous studies.[28,29] In our case, plaque rupture is likely to happen towards the ends of plaque region, a condition that can lead to heart attack (coronary artery) or stroke (carotid artery). In addition, there could be local damage to plaque/artery where the high stresses are located. This condition also leads to the growth of new tissue, e.g. proliferation of smooth muscle cells, around the stent, causing in-stent restenosis.
Figure 9. Contour plot of the von Mises stress (MPa) on (A) Elixir and (B) Xience stents after deployment
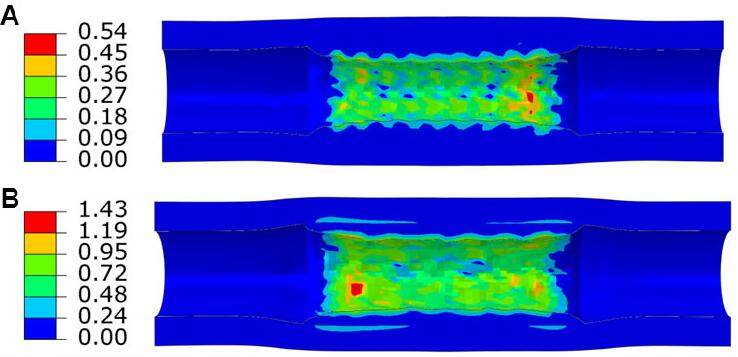
The maximum principal stress on the plaque had a peak value of 1.43 MPa and 0.54 MPa for the Xience and Elixir stents, respectively [Figure 10]. The considerably lower stress level for Elixir stent is consistent with the reduced property mismatch between the polymer and the artery as well as less arterial expansion achieved by the polymer stent. It should be noted that stress triaxiality was not explored for the stents and diseased artery. Stress triaxiality is defined as the ratio of hydrostatic stress to the equivalent (or von Mises) stress, and it is a key parameter used in ductile fracture analysis. In this study, we mainly focus on the stress state of stent-artery system during crimping and expansion, instead of fracture or failure. Consequently, stress triaxiality is not presented. But we aim to look into this in future studies when considering the failure and fracture of stent, plaque and arteries in the simulations.
Effect of residual stresses caused by crimping
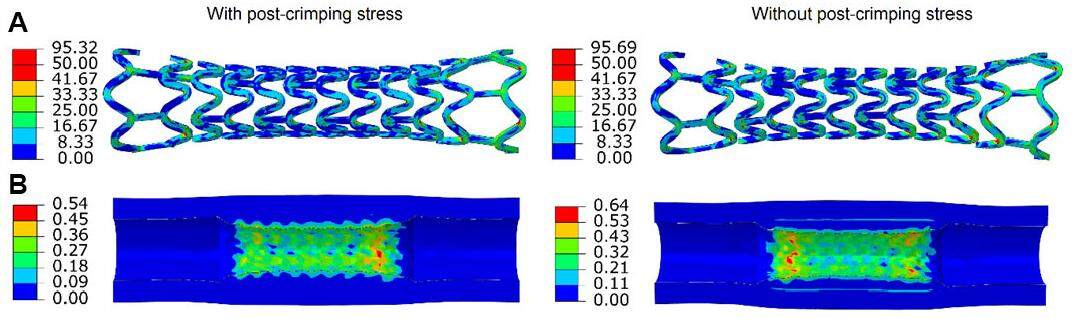
As shown in Figure 7, crimping introduced severe residual stresses into the stent, which can affect the subsequent expansion of the device. To understand such effect, simulations of stent deployment were also carried out for both stents without including the residual stresses generated from crimping.
For Elixir stent, it is confirmed that crimping-caused residual stresses do affect stent expansion [Figure 11]. When stent expansion was simulated without considering residual stress, the stent expanded faster and reached saturation earlier, as shown by the solid blue line in Figure 11A. Overall, residual stresses tend to compromise stent expansion both at peak pressure and after balloon deflation. At peak pressure, stent outer diameter was found to be 2.61 mm and 2.75 mm for simulations with and without considering residual stresses, respectively, and settled as 2.10 mm and 2.19 mm, respectively, after balloon deflation. Although the recoiling had similar magnitude for both cases (~20%; with and without residual stresses), less dogboning was found when residual stresses were excluded in simulations (i.e. 41%; versus 45% for simulations with residual stresses). As shown in Figure 12, residual stresses did not affect the pattern of stress distribution in the stent and artery. On the stent, stresses are still highly localised at the U-bend regions, regardless of the residual stress state. Also, the maximum stress on the stent changed only by ~0.4% (95.69 to 95.32 MPa) when residual stresses were considered in the simulations. In the artery [Figure 12B], stresses were again concentrated towards the ends of the plaque as a result of stent dogboning effect. The peak value of the maximum principal stress changed by ~15% (0.64 to 0.54 MPa) when the residual stresses were included.
Figure 11. (A) Diameter change against pressure; and (B) recoiling and dogboning effects obtained from simulations with and without considering crimping-caused post-crimping stresses on Elixir stent
Figure 12. (A) von Mises stress (MPa) on the Elixir stent; and (B) maximum principal stress (MPa) on the artery-plaque system for simulations with (left) and without (right) considering residual stresses
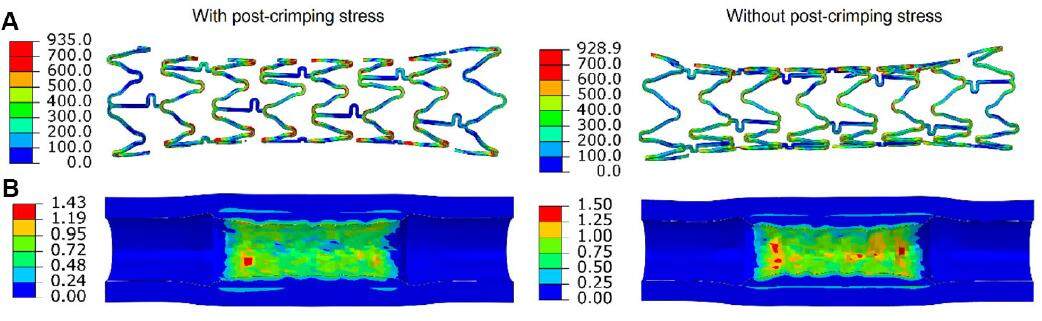
For Xience stent, residual stresses affected the early stage of expansion of the stent as shown in Figure 13. The achieved final diameter (~2.40 mm) and the recoiling effect (~11%) were similar for the two cases (with and without residual stresses). Dogboning increased when residual stresses were excluded, with a value of 36% (compared to 24% for the case considering residual stresses). As shown in Figure 14, the stresses developed in the stent and the diseased artery were similar, in terms of distribution, for the two cases (with and without residual stresses). In terms of magnitude, the maximum stress in the stent changed only by ~0.7% (928.9 to 935.0 MPa) when residual stresses were included in the simulations. For the diseased artery, the peak value of the maximum principal stress changed by ~5% (1.50 MPa to 1.43 MPa) when the residual stresses were considered.
Figure 13. (A) Diameter change against pressure; and (B) recoiling and dogboning effects obtained from simulations with and without considering crimping-caused residual stresses on Xience stent
Discussion
Clinically, in-stent restenosis (ISR), i.e. re-narrowing of stented artery, is one of the major drawbacks associated with stent implantation.[30] ISR is a direct consequence of the formation of neointima, largely caused by proliferating smooth muscle cells and accumulated extracellular matrix.[30] According to recent investigations, arterial wall biomechanics plays a key role in ISR. The stenting-caused alteration of biomechanical environment controls the inflammatory and remodelling processes of vessel walls. As reported by Timmins et al.,[31] stent designs that induced higher levels of non-physiologic stresses provoked a more aggressive pathobiological response of the vessel walls, leading to a higher degree of neointimal formation. In-vitro studies have also proved that mechanical stresses regulated the proliferation and migration of vascular cells,[32] and the synthesis and reorganization of extracellular matrix.[33] Stent-induced vessel stresses are closely linked with the level of artery injury, also promoting the development of restenosis. From this study, it is clear that the stresses in the artery appear to be largely affected by the stent materials and designs. PLLA has lower modulus, yield strength and strain hardening, which soothed the stent-artery interaction and led to stress reduction in vessel layers as shown in Figure 10. This is clinically beneficial. Bioresorbable polymeric stents are also more compliant than metallic stents, diminishing associated vascular responses over the scaffolded vessel segments.[34]
Residual stresses in stents were studied by Möller et al.[35] using X-ray diffraction method. Their work confirmed that even for as-produced stents, a significant amount of microstresses can be developed in the stent during crimping (this is also the case found in our work). Subsequent stent expansion caused an increase of stress due to tension. According to their study, the level of stresses introduced by crimping and expansion can considerably affect the fatigue life of the stent. Based on our results, crimping and expansion processes were found to induce comparable levels of stresses in the stent struts. Also, residual stresses developed during crimping affected the expansion behaviour, though only slightly, of stent in the deployment step. It is also thought that residual stresses in the stent contributed to the flexibility of the device, thus imposing less stresses on the plaque during further deformation as confirmed by our simulation results, although only marginally.
The targeted vessel diameter (i.e. 3 mm) could not be achieved by stent expansion only. This is the case for both polymer and metallic stents. Firstly, it was due to the saturated expansion of the artery layers, developed at a later stage of vessel stretching. This happened when the stiffness of vessel layers, especially the intima layer, increased steeply upon large stretch [Figure 4]. Secondly, vessel layers were assumed to deform purely elastically which imposed a large recovery force on the expanded stent after balloon deflation. Generally, the expansion of polymer stent was slower than that of metallic stent. Higher recoiling was also observed for polymeric stent due to the weaker mechanical properties. This indicates that there is a challenge to use polymer stents to achieve desired lumen diameter, especially for patients with stiffer artery and heavily calcified plaques. However, it is recognised that polymer stent induced significantly lower stresses in the artery than metallic stents, which could reduce the occurrence of arterial injuries and in-stent restenosis.
In clinical practice, most stents are post-dilated with relatively non-compliant balloons, i.e. stiffer and larger than the stent delivery system balloon, to ensure good apposition and to ensure that the intended diameter is achieved. However, multiple cycles of inflation were not simulated here which is a limitation of this study. The simulation in this work was a single deployment of stent or direct stenting of a vascular lesion. In clinical practice, pre-dilatation of diseased artery can also occur. Direct-stenting is common, but not with bioresorbable polymer stents. For bioresorbable polymer stents (or any new technology), the users generally acknowledge the importance of careful lesion preparation by pre-dilatation as well as post-dilatation. The pre-dilatation balloon inflation step modifies the plaque and results in less recoil after deployment of a stent or scaffold. After a stent is deployed, an additional post-dilatation generally occurs with a second larger balloon. Sometimes this is to achieve a better deployment through a tapered vessel, or to "crack" a stubborn plaque. Sometimes, this is required when two stents are deployed with an overlap. This type of balloon pre-dilatation and post-dilatation is essential for polymer stents to be effective in difficult lesions. In fact, larger degrees of recoil and dogboning predicted by the simulations indicate that adequate pre-dilatation and post-dilatation are potentially critical for polymeric stents to achieve optimal clinical results. Simulation of pre-dilation or post-dilation requires proper inelastic or damage models to describe unrecoverable deformation for the plaque and artery wall, which is currently beyond the scope of the paper. In this study, the artery and plaque were assumed to behave purely elastically (hyperelastic model), and the efforts of pre-dilation or post-dilation will be nullified as soon as the dilation pressure is removed. Modelling of inelastic deformation and damage will be attempted in our future work.
In addition, the stresses in the vessel layers at peak inflating pressure are generally beyond the ultimate tensile strength of the tissue layer.[25] This is also the case for the plaques. Therefore, tissue damage will need to be modelled in the FE simulations at high pressure levels. Tissue damage is associated with unrecoverable deformation in the artery, which could reduce the stent recoiling considerably upon balloon deflation. Consequently, stent is expected to expand further if tissue damage is considered due to irrecoverable mechanical deformation of the artery-plaque system, thus resulting in a larger lumen diameter. Damage modeling of arterial layers is a limitation of this study and will be studied in our future work. However, it does not affect the general conclusion of this paper, as we aim to make like-for-like comparison of the scaffolding capability and mechanical performance between bioresorbable polymeric and metallic stents.
On the other hand, the plaque can be classified as hypocellular, cellular or calcified, depending on the composition. It is more difficult to treat calcified plaque by stenting due to its strong resistance to stretch when compared to hypocellular or cellular plaques.[18] So far, the effect of plaque composition on stent expansion was only evaluated for isotropic tissue model, and further work is required to study such effects by considering vessel anisotropy. Finally, polymers generally possess anisotropy and viscoplasticity effects which could also affect the simulation results and will need to be addressed in future studies.
In conclusion, crimping and deployment of polymeric and metallic stents have been simulated using finite element method to give a direct comparison of their mechanical performances. Results demonstrated that polymer stent has a lower rate of expansion than metallic stent. The overall expansion, reached at peak inflating pressure and after balloon deflation, was lower for polymer stent due to weaker material properties. This is also associated with the higher recoiling effect for polymer stent. Thus, it is a challenge to use polymer stent to treat patients with heavily calcified plaques or stiffer vessels, without pre-dilation or post-dilation. Crimping generated severe residual stresses in the stent, which tend to affect stent expansion and increase dogboning for Elixir polymer stent. However, they did not alter the stress distribution during the deployment process, and only imposed small changes to the stress magnitude.
Declarations
Financial support and sponsorshipNil.
Conflicts of interestThere are no conflicts of interest.
Patient consentThere is no patient involved.
Ethics approvalThis article does not contain any studies with human participants or animals.
REFERENCES
1. Hoffmann R, Mintz GS. Coronary in-stent restenosis - predictors, treatment and prevention. Eur Heart J 2000;21:1739-49.
2. Joner M, Finn AV, Farb A, Mont EK, Kolodgie FD, Ladich E, Kutys R, Skorija K, Gold HK, Virmani R. Pathology of drug-eluting stents in humans: delayed healing and late thrombotic risk. J Am Coll Cardiol 2006;48:193-202.
3. Yang TH, Kim DI, Park SG, Seo JS, Cho HJ, Seol SH, Kim SM, Kim DK, Kim DS. Clinical characteristics of stent fracture after sirolimus-eluting stent implantation. Int J Cardiol 2009;131:212-6.
4. Flege C, Vogt F, Höges S, Jauer L, Borinski M, Schulte VA, Hoffmann R, Poprawe R, Meiners W, Jobmann M, Wissenbach K, Blindt R. Development and characterization of a coronary polylactic acid stent prototype generated by selective laser melting. J Mater Sci Mater Med 2013;24:241-55.
6. Onuma Y, Serruys PW. Bioresorbable scaffold: the advent of a new era in percutaneous coronary and peripheral revascularization? Circulation 2011;123:779-97.
7. Waksman R. Biodegradable stents: they do their job and disappear. J Invasive Cardiol 2006;18:70-4.
8. Serruys PW, Chevalier B, Dudek D, Cequier A, Carrié D, Iniguez A, Dominici M, van der Schaaf RJ, Haude M, Wasungu L, Veldhof S, Peng L, Staehr P, Grundeken MJ, Ishibashi Y, Garcia-Garcia HM, Onuma Y. A bioresorbable everolimus-eluting scaffold versus a metallic everolimus-eluting stent for ischaemic heart disease caused by de-novo native coronary artery lesions (ABSORB II): an interim 1-year analysis of clinical and procedural secondary outcomes from a randomised controlled trial. Lancent 2015;385:43-54.
9. Gao R, Abizaid A, Banning A, Bartorelli AL, DŽavík V, Ellis S, Jeong MH, Legrand V, Spaulding C, Urban P. One-year outcome of small-vessel disease treated with sirolimus-eluting stents: a subgroup analysis of the e-SELECT registry. J Interv Cardiol 2013;26:163-72.
10. Agrawal CM, Haas KF, Leopold DA, Clark HG. Evaluation of poly (L-lactic acid) as a material for intravascular polymeric stents. Biomaterials 1992;13:176-82.
11. Nuutinen JP, Clerc C, Reinikainen R, Törmälä P. Mechanical properties and in vitro degradation of bioabsorbable self-expanding braided stents. J Biomater Sci Polym Ed 2003;14:255-66.
12. Bünger CM, Grabow N, Sternberg K, Kröger C, Ketner L, Schmitz KP, Kreutzer HJ, Ince H, Nienaber CA, Klar E, Schareck W. Sirolimus-eluting biodegradable poly-L-lactide stent for peripheral vascular application: a preliminary study in porcine carotid arteries. J Surg Res 2007;139:77-82.
13. Verheye S, Ormiston JA, Stewart J, Webster M, Sanidas E, Costa R, Costa Jr JR, Chamie D, Abizaid AS, Pinto I, Morrison L, Toyloy S, Bhat V, Yan J, Abizaid A. A next-generation bioresorbable coronary scaffold system: from bench to first clinical evaluation: 6-and 12-month clinical and multimodality imaging results. JACC Cardiovasc Interv 2014;7:89-99.
14. Chua SND, MacDonald BJ, Hashmi MSJ. Finite element simulation of stent and balloon interaction. J Mater Process Technol 2003;143-144:591-7.
15. Lally C, Dolan F, Prendergast PJ. Cardiovascular stent design and vessel stresses: a finite element analysis. J Biomech 2005;38:1574-81.
16. Gijsen FJ, Migliavacca F, Schievano S, Socci L, Petrini L, Thury A, Wentzel JJ, van der Steen AF, Serruys PW, Dubini G. Simulation of stent deployment in a realistic human coronary artery. Biomed Eng Online 2008;7:23.
17. Imani SM, Goudarzi AM, Ghasemi SE, Kalani A, Mahdinejad J. Analysis of the stent expansion in a stenosed artery using finite element method: application to stent versus stent study. Proc Inst Mech Eng H 2014;228:996-1004.
18. Schiavone A, Zhao LG, Abdel-Wahab AA. Effects of material, coating, design and plaque composition on stent deployment inside a stenotic artery -- finite element simulation. Mater Sci Eng C Mater Biol Appl 2014;42:479-88.
19. Clune R, Kelliher D, Robinson JC, Campbell JS. NURBS modeling and structural shape optimization of cardiovascular stents. Struct Multidiscipl Optim 2014;50:159-68.
20. Pauck RG, Reddy BD. Computational analysis of the radial mechanical performance of PLLA coronary artery stents. Med Eng Phys 2015;37:7-12.
21. Medtronic Technical Bulletin (2003) Advantages of cobalt alloy for coronary stents. Available from: http://wwwp.medtronic.com/newsroom/content/1110132739468.pdf [Last Accessed on 11-01-2017].
22. Zahedmanesh H, Lally C. Determination of the influence of stent strut thickness using the finite element method: implications for vascular injury and in-stent restenosis. Med Biol Eng Comput 2009;47:385-93.
23. Gervaso F, Capelli C, Petrini L, Lattanzio S, Di Virgilio L, Migliavacca F. On the effects of different strategies in modelling balloon-expandable stenting by means of finite element method. J Biomech 2008;41:1206-12.
24. Holzapfel GA, Gasser TC, Ogden RW. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J Elast Phys Sci Solids 2000;61:1-48.
25. Holzapfel GA, Sommer G, Gasser CT, Regitnig P. Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling. Am J Physiol Heart Circ Physiol 2005;289:H2048-58.
26. Nolan DR, Gower AL, Destrade M, Ogden RW, McGarry JP. A robust anisotropic hyperelastic formulation for the modelling of soft tissue. J Mech Behav Biomed Mater 2014;39:48-60.
27. Migliavacca F, Petrini L, Colombo M, Auricchio F, Pietrabissa R. Mechanical behavior of coronary stents investigated through the finite element method. J Biomech 2002;35:803-11.
28. Cheng GC, Loree HM, Kamm RD, Fishbein MC, Lee RT. Distribution of circumferential stress in ruptured and stable atherosclerotic lesions. A structural analysis with histopathological correlation. Circulation 1993;87:1179-87.
29. Li ZY, Howarth S, Trivedi RA, U-King-Im JM, Graves MJ, Brown A, Wang L, Gillard JH. Stress analysis of carotid plaque rupture based on in vivo high resolution MRI. J Biomech 2006;39:2611-22.
30. Lowe HC, Oesterle SN, Khachigian LM. Coronary in-stent restenosis: current status and future strategies. J Am Coll Cardiol 2002;39:183-93.
31. Timmins LH, Miller MW, Clubb FJ Jr, Moore JE Jr. Increased artery wall stress post-stenting leads to greater intimal thickening. Lab Invest 2011;91:955-67.
32. Haga JH, Li YS, Chien S. Molecular basis of the effects of mechanical stretch on vascular smooth muscle cells. J Biomech 2007;40:947-60.
33. Chung IM, Gold HK, Schwartz SM, Ikari Y, Reidy MA, Wight TN. Enhanced extracellular matrix accumulation in restenosis of coronary arteries after stent deployment. J Am Coll Cardiol 2002;40:2072-81.
34. Sharkawi T, Cornhill F, Lafont A, Sabaria P, Vert M. Intravascular bioresorbable polymeric stents: a potential alternative to current drug eluting metal stents. J Pharm Sci 2007;96:2829-37.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Schiavone A, Qiu TY, Zhao LG. Crimping and deployment of metallic and polymeric stents -- finite element modelling. Vessel Plus 2017;1:12-21. http://dx.doi.org/10.20517/2574-1209.2016.03
AMA Style
Schiavone A, Qiu TY, Zhao LG. Crimping and deployment of metallic and polymeric stents -- finite element modelling. Vessel Plus. 2017; 1: 12-21. http://dx.doi.org/10.20517/2574-1209.2016.03
Chicago/Turabian Style
Schiavone, Alessandro, Tian-Yang Qiu, Li-Guo Zhao. 2017. "Crimping and deployment of metallic and polymeric stents -- finite element modelling" Vessel Plus. 1: 12-21. http://dx.doi.org/10.20517/2574-1209.2016.03
ACS Style
Schiavone, A.; Qiu T.Y.; Zhao L.G. Crimping and deployment of metallic and polymeric stents -- finite element modelling. Vessel Plus. 2017, 1, 12-21. http://dx.doi.org/10.20517/2574-1209.2016.03
About This Article
Copyright
Author Biographies

Data & Comments
Data
 Cite This Article 29 clicks
Cite This Article 29 clicks













Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.